[Programmers] 배달 (Python3)

문제

N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.

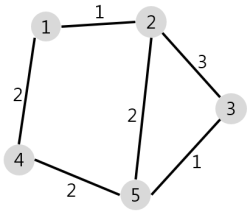
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.

마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.

제한사항

• 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
• road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
• road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
• road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
• a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
• 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
• 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
• K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
• 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
• 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.

  입출력 예

  |N |road |K |result|
  |:—:|:—:|:—:|:—:|
  |5 |[[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]] |3 |4|
  |6 |[[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]]|4| 4

입출력 예 설명

입출력 예 #1
문제의 예시와 같습니다.

입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.

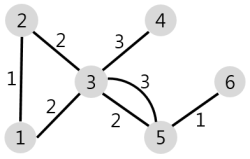
1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.

문제풀이

맨 처음에는 bfs나 dfs로 풀려고 했는데, 아무리 풀어봐도 거리를 저장하는게 어려워서 해답을 찾아봤다. 이 문제는 다익스트라 알고리즘(dijkstra algorithm) 으로 푸는 문제로, 다익스트라 알고리즘은 최단거리를 구할 때 사용하는 알고리즘이다. 보통 노드와 노드, 그리고 노드 사이의 거리 or 시간의 세가지가 주어질 때 사용하는 알고리즘으로, 힙큐와 bfs를 일정 부분 섞어서 사용하는 알고리즘이다.

다익스트라 알고리즘은 그리디 알고리즘의 한 종류로, 매 상황에서 가장 비용이 적은 노드를 선택해 과정을 반복함으로써 얻은 최단 경로가 실제로 가장 비용이 적은 노드가 해답이라는 가정하에 사용한다.

알고리즘의 동작 과정은 다음과 같다.

1. 출발 노드를 설정한다.
2. 최단 거리 테이블을 초기화한다.
3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택한다.
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
5. 3번과 4번을 반복한다.

코드

from collections import deque
import heapq
import sys
INF = sys.maxsize

def solution(N, road, K):
    distance = [INF]*(N+1)
    graph = [[] for _ in range(N+1)]
    for i in road:
        graph[i[0]].append((i[1],i[2]))
        graph[i[1]].append((i[0],i[2]))
    
    def dijkstra(start):
        q = []
        heapq.heappush(q,(0,start))
        distance[start] = 0
        while q:
            dist, now = heapq.heappop(q)
            if distance[now] < dist:
                continue
            for i in graph[now]:
                cost = dist+i[1]
                if cost < distance[i[0]]:
                    distance[i[0]] = cost
                    heapq.heappush(q,(cost,i[0]))
    dijkstra(1)
    result = 0
    for i in range(1, N+1):
        if distance[i] <= K:
            result += 1
        
    return result

solution(5,[[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]],3)

[[], [(2, 1), (4, 2)], [(1, 1), (3, 3), (5, 2)], [(2, 3), (5, 1)], [(1, 2), (5, 2)], [(2, 2), (3, 1), (4, 2)]]





4